Теория вероятностей
Работа с неопределенностью и вероятностные модели в машинном обучении
Теория вероятностей в машинном обучении
Теория вероятностей предоставляет математический аппарат для работы с неопределенностью, которая присутствует во всех реальных данных. В машинном обучении вероятностные методы позволяют моделировать неопределенность в данных, делать предсказания с оценкой уверенности и обновлять убеждения на основе новых наблюдений.
Почему теория вероятностей важна для AI?
Реальные данные всегда содержат шум и неопределенность. Измерения могут быть неточными, данные могут быть неполными, и будущие события по своей природе непредсказуемы. Теория вероятностей дает нам инструменты для количественной оценки и работы с этой неопределенностью.
Многие модели машинного обучения являются вероятностными. Вместо того чтобы предсказывать точное значение, они предсказывают распределение вероятностей. Например, модель классификации изображений не просто говорит "это кошка", а говорит "с вероятностью 85% это кошка, с вероятностью 10% это собака, с вероятностью 5% это что-то другое". Это более информативно и честно отражает неопределенность модели.
Байесовские методы, основанные на теореме Байеса, позволяют систематически обновлять наши убеждения по мере получения новых данных. Это мощный подход, который находит применение во многих областях машинного обучения, от фильтрации спама до автономных транспортных средств.
Основные концепции
Рассмотрим фундаментальные понятия теории вероятностей, необходимые для машинного обучения.
Основы вероятности
Вероятность - это число от 0 до 1, которое измеряет степень уверенности в том, что событие произойдет. Вероятность 0 означает, что событие точно не произойдет, вероятность 1 - что точно произойдет. Промежуточные значения отражают степень неопределенности.
Условная вероятность P(A|B) - это вероятность события A при условии, что событие B уже произошло. Это ключевая концепция для понимания зависимостей между событиями и для байесовского вывода.
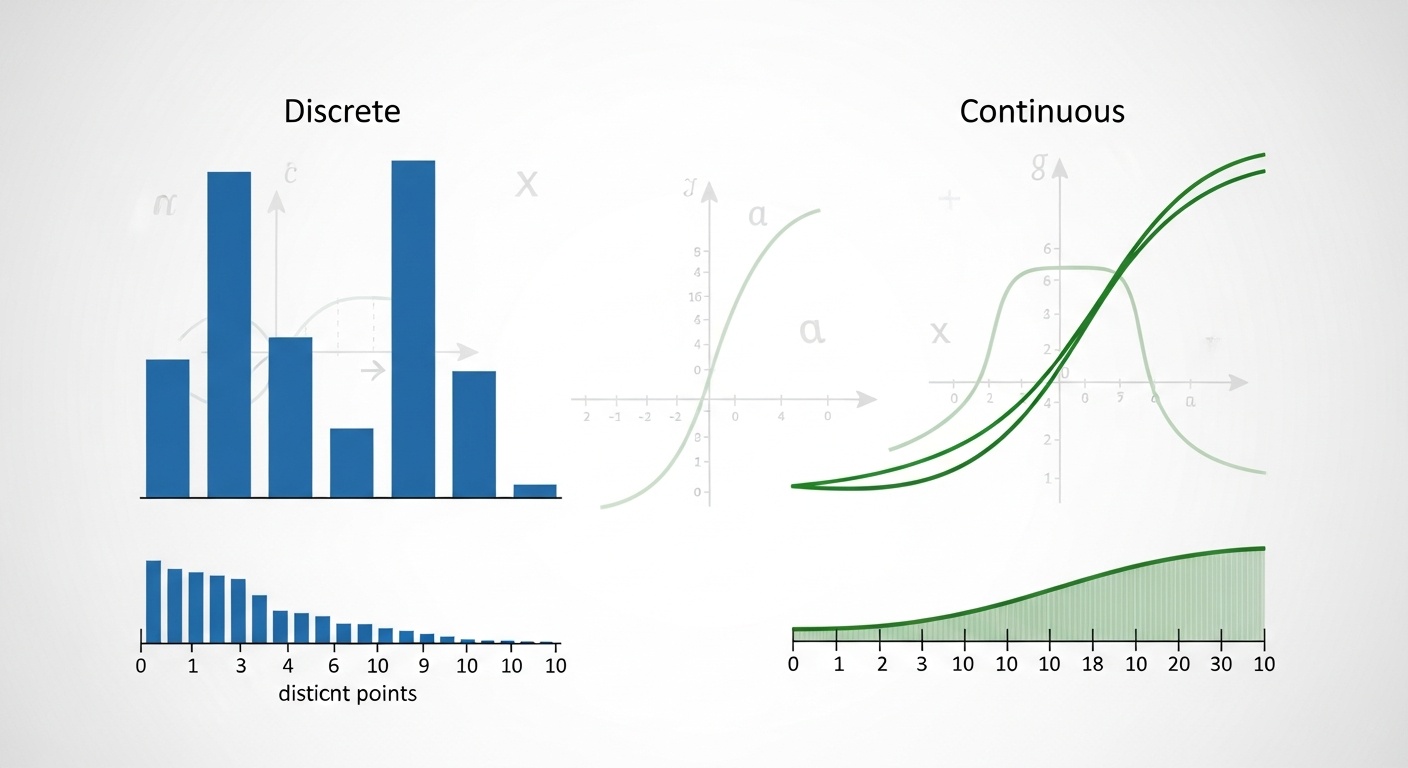
Распределения вероятностей
Распределение вероятностей описывает, как вероятность распределена между возможными значениями случайной величины. Для дискретных величин это функция вероятности, для непрерывных - функция плотности вероятности.
Нормальное (гауссово) распределение - одно из самых важных в машинном обучении. Многие явления в природе и данных приближенно следуют нормальному распределению благодаря центральной предельной теореме.
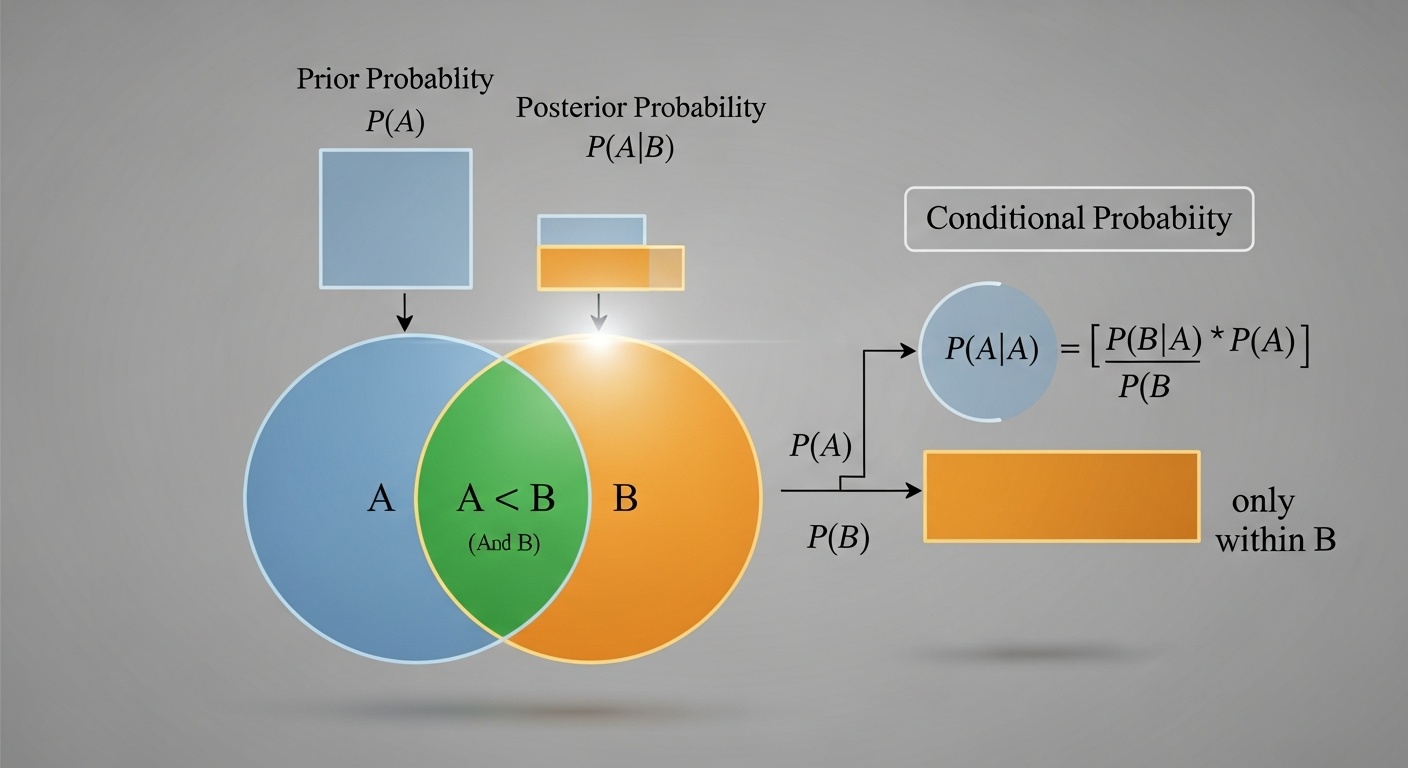
Теорема Байеса
Теорема Байеса показывает, как обновлять вероятность гипотезы на основе новых данных: P(H|D) = P(D|H) × P(H) / P(D). Это фундаментальная формула для байесовского вывода и машинного обучения.
P(H|D) - апостериорная вероятность (после наблюдения данных), P(H) - априорная вероятность (до наблюдения данных), P(D|H) - правдоподобие (вероятность данных при данной гипотезе). Теорема показывает, как комбинировать априорные знания с новыми данными.

Математическое ожидание и дисперсия
Математическое ожидание (среднее значение) случайной величины - это взвешенное среднее всех возможных значений, где веса - это вероятности. Оно характеризует "центр" распределения.
Дисперсия измеряет разброс значений вокруг среднего. Большая дисперсия означает, что значения сильно разбросаны, малая - что они сконцентрированы около среднего. Стандартное отклонение - это квадратный корень из дисперсии.
Применение в машинном обучении
Теория вероятностей находит множество применений в машинном обучении. Рассмотрим основные из них.
Вероятностная классификация
Многие алгоритмы классификации являются вероятностными. Вместо жесткого отнесения объекта к одному классу, они предсказывают вероятность принадлежности к каждому классу. Например, логистическая регрессия моделирует вероятность принадлежности к классу как функцию признаков.
Наивный байесовский классификатор использует теорему Байеса для вычисления вероятности класса при данных признаках. Несмотря на "наивное" предположение о независимости признаков, этот метод часто работает удивительно хорошо на практике, особенно для классификации текстов.
Генеративные модели
Генеративные модели моделируют совместное распределение признаков и меток P(X, Y). Это позволяет не только классифицировать объекты, но и генерировать новые примеры. Например, генеративные состязательные сети (GAN) могут создавать реалистичные изображения, обучившись на реальных данных.
Вариационные автоэнкодеры (VAE) - еще один пример генеративных моделей. Они изучают вероятностное представление данных в низкоразмерном пространстве, что позволяет генерировать новые примеры и выполнять интерполяцию между существующими примерами.
Байесовская оптимизация
Байесовская оптимизация - это эффективный метод для оптимизации дорогих "черных ящиков" функций, таких как гиперпараметры моделей машинного обучения. Метод использует вероятностную модель (обычно гауссовский процесс) для моделирования функции и выбора следующей точки для оценки.
В отличие от случайного поиска или перебора по сетке, байесовская оптимизация использует информацию из предыдущих оценок для интеллектуального выбора следующих точек. Это позволяет найти хорошие гиперпараметры с меньшим количеством оценок.
Оценка неопределенности
Вероятностные модели позволяют не только делать предсказания, но и оценивать неопределенность этих предсказаний. Это критично для приложений, где ошибки могут иметь серьезные последствия, таких как медицинская диагностика или автономное вождение.
Байесовские нейронные сети моделируют распределение вероятностей над весами сети, что позволяет получить распределение предсказаний. Это дает более полную картину неопределенности модели по сравнению с точечными оценками обычных нейронных сетей.
Важные распределения
Некоторые распределения вероятностей особенно важны для машинного обучения.
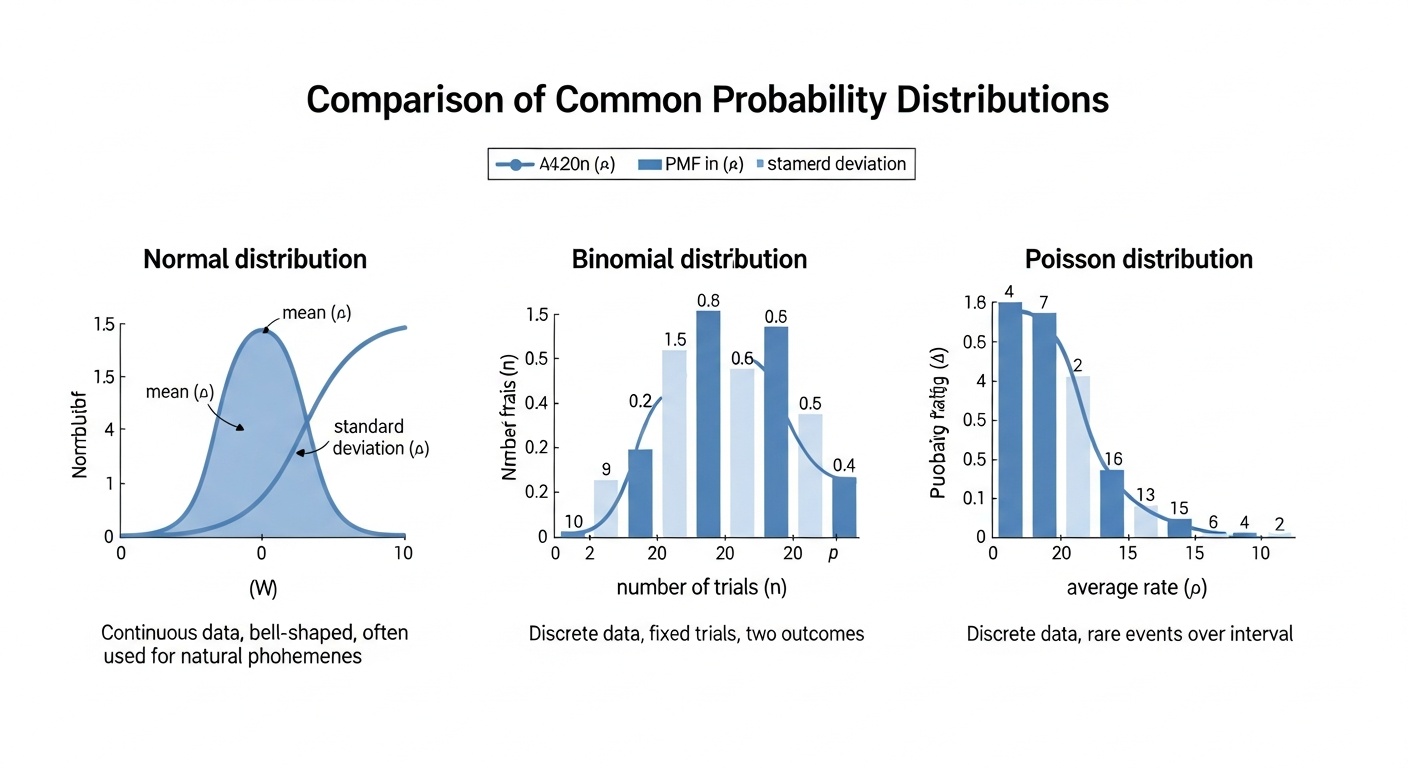
Нормальное распределение
Симметричное колоколообразное распределение, характеризуемое средним и стандартным отклонением. Многие явления в природе следуют нормальному распределению. Широко используется в машинном обучении для моделирования шума и ошибок.
Биномиальное распределение
Распределение количества успехов в серии независимых испытаний Бернулли. Используется для моделирования бинарных событий, таких как клик/не клик, покупка/не покупка. Основа для логистической регрессии.
Распределение Пуассона
Моделирует количество событий, происходящих в фиксированном интервале времени или пространства. Используется для моделирования редких событий, таких как количество посетителей сайта в час или количество дефектов на производстве.
Экспоненциальное распределение
Моделирует время между событиями в пуассоновском процессе. Используется для моделирования времени жизни, времени ожидания и других временных интервалов. Имеет свойство отсутствия памяти.
Бета-распределение
Распределение на интервале [0, 1], часто используется для моделирования вероятностей и пропорций. Является сопряженным априорным распределением для биномиального распределения в байесовском выводе.
Многомерное нормальное
Обобщение нормального распределения на многомерный случай. Характеризуется вектором средних и ковариационной матрицей. Используется в гауссовских процессах и многих других вероятностных моделях.
Максимальное правдоподобие
Метод максимального правдоподобия - это один из основных методов оценки параметров вероятностных моделей. Идея проста: выбрать параметры модели так, чтобы наблюдаемые данные были наиболее вероятными.
Формально, мы максимизируем функцию правдоподобия L(θ|D) = P(D|θ), которая показывает вероятность данных D при параметрах θ. На практике часто максимизируют логарифм правдоподобия, что математически эквивалентно, но вычислительно удобнее.
Многие алгоритмы машинного обучения можно интерпретировать как методы максимального правдоподобия. Например, обучение нейронной сети с функцией потерь кросс-энтропии эквивалентно максимизации правдоподобия при предположении, что данные следуют категориальному распределению.
Важное уведомление: Этот сайт носит исключительно информационный характер и не предоставляет образовательных услуг.
Пожалуйста, ознакомьтесь с нашими Отказом от ответственности и Политикой конфиденциальности.
