Математический анализ
Производные, градиенты и оптимизация - инструменты обучения нейронных сетей
Роль математического анализа в машинном обучении
Математический анализ, особенно дифференциальное исчисление, является основой для понимания того, как обучаются модели машинного обучения. Производные и градиенты позволяют нам понять, как изменяется функция при изменении ее параметров, что критично для оптимизации моделей и поиска наилучших параметров.
Почему математический анализ критичен для AI?
В основе машинного обучения лежит задача оптимизации: мы хотим найти параметры модели, которые минимизируют функцию потерь. Функция потерь измеряет, насколько хорошо модель справляется с задачей. Чтобы минимизировать эту функцию, нам нужно знать, в каком направлении двигаться в пространстве параметров.
Именно здесь на помощь приходит математический анализ. Производная функции показывает, как быстро и в каком направлении функция изменяется. Градиент - это многомерное обобщение производной - показывает направление наибыстрейшего возрастания функции. Двигаясь в противоположном направлении (градиентный спуск), мы можем найти минимум функции.
Без понимания производных и градиентов невозможно понять, как работает обучение нейронных сетей. Алгоритм обратного распространения ошибки, который лежит в основе обучения глубоких нейронных сетей, полностью основан на вычислении градиентов с помощью цепного правила дифференцирования.
Основные концепции
Рассмотрим ключевые понятия математического анализа, необходимые для понимания машинного обучения.
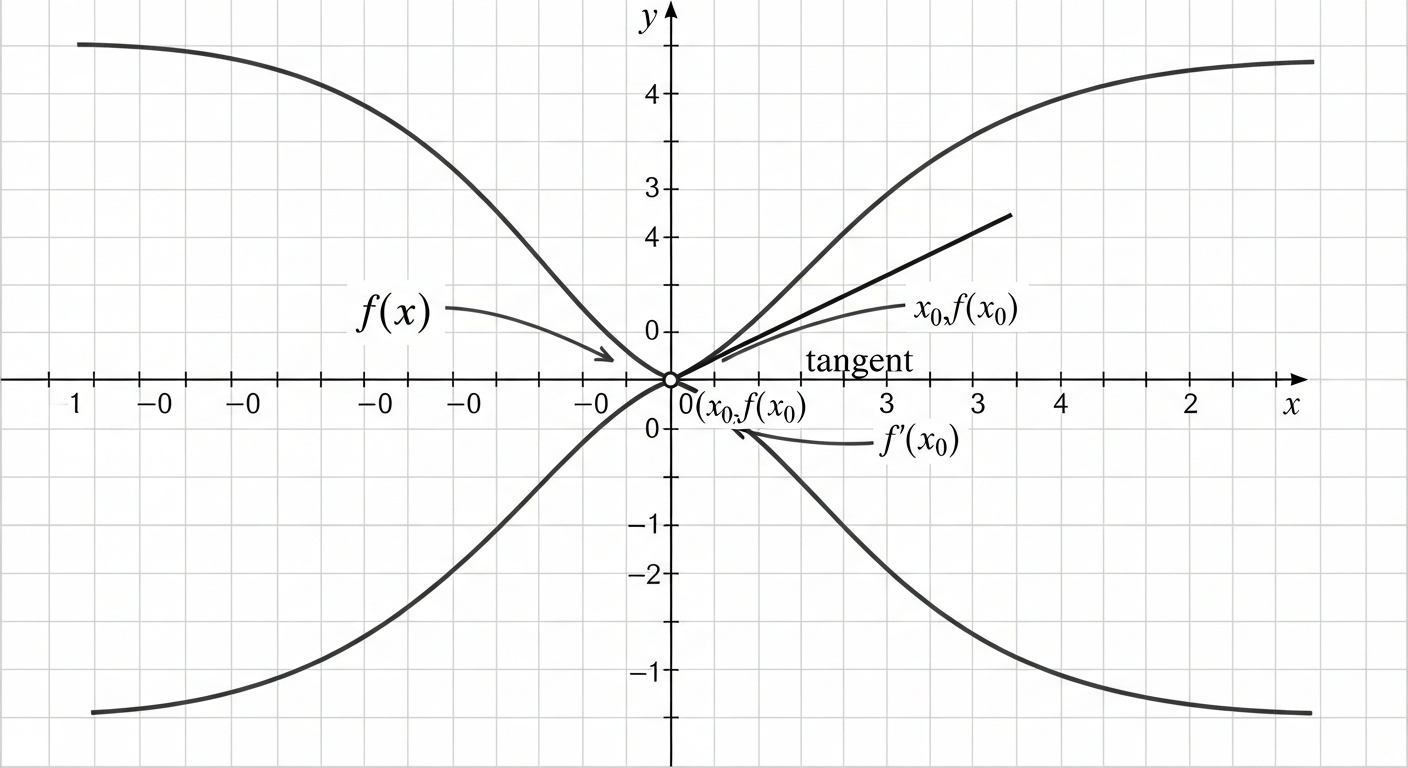
Производные
Производная функции показывает скорость изменения функции в данной точке. Геометрически это наклон касательной к графику функции. В машинном обучении производные используются для определения, как изменение параметров модели влияет на функцию потерь.
Понимание производных позволяет нам оптимизировать модели: мы можем определить, в каком направлении нужно изменить параметры, чтобы уменьшить ошибку модели. Это фундаментальная идея, лежащая в основе всех алгоритмов обучения с учителем.

Градиенты
Градиент - это вектор частных производных функции многих переменных. Он указывает направление наибыстрейшего возрастания функции. В машинном обучении градиент функции потерь по параметрам модели показывает, как нужно изменить параметры для увеличения потерь.
Двигаясь в направлении, противоположном градиенту (градиентный спуск), мы уменьшаем функцию потерь и улучшаем модель. Это основной алгоритм обучения нейронных сетей и многих других моделей машинного обучения.

Цепное правило
Цепное правило позволяет вычислять производную сложной функции, представленной как композицию более простых функций. Это критично для нейронных сетей, которые представляют собой композицию множества функций (слоев).
Алгоритм обратного распространения ошибки использует цепное правило для эффективного вычисления градиентов по всем параметрам сети. Без цепного правила обучение глубоких нейронных сетей было бы вычислительно невозможным.
Оптимизация
Оптимизация - это процесс поиска минимума или максимума функции. В машинном обучении мы оптимизируем функцию потерь, чтобы найти наилучшие параметры модели. Производные и градиенты являются основными инструментами оптимизации.
Существует множество алгоритмов оптимизации: градиентный спуск, стохастический градиентный спуск, Adam, RMSprop и другие. Все они основаны на использовании градиентов для итеративного улучшения параметров модели.
Градиентный спуск
Градиентный спуск - это основной алгоритм оптимизации в машинном обучении. Давайте разберем, как он работает.
Шаг 1: Инициализация
Алгоритм начинается с случайной инициализации параметров модели. Это может быть любая точка в пространстве параметров. Выбор начальной точки может влиять на то, какой локальный минимум будет найден, но для многих задач это не критично.
Важно правильно выбрать масштаб инициализации. Слишком большие начальные значения могут привести к нестабильности обучения, а слишком малые - к медленной сходимости. Существуют специальные методы инициализации, такие как Xavier или He инициализация, которые учитывают архитектуру сети.
Шаг 2: Вычисление градиента
На каждой итерации мы вычисляем градиент функции потерь по параметрам модели. Градиент показывает направление наибыстрейшего возрастания функции потерь. Для нейронных сетей градиент вычисляется с помощью алгоритма обратного распространения ошибки.
Вычисление градиента - это самая вычислительно затратная часть обучения. В современных фреймворках глубокого обучения (TensorFlow, PyTorch) градиенты вычисляются автоматически с помощью автоматического дифференцирования, что значительно упрощает разработку моделей.
Шаг 3: Обновление параметров
Параметры обновляются в направлении, противоположном градиенту: новые_параметры = старые_параметры - скорость_обучения × градиент. Скорость обучения (learning rate) - это гиперпараметр, который контролирует размер шага.
Выбор правильной скорости обучения критичен. Слишком большая скорость может привести к расхождению алгоритма, а слишком малая - к очень медленному обучению. Часто используются адаптивные методы, которые автоматически подстраивают скорость обучения в процессе обучения.
Шаг 4: Повторение
Шаги 2 и 3 повторяются до тех пор, пока не будет достигнут критерий остановки. Это может быть достижение определенного значения функции потерь, максимальное количество итераций, или отсутствие улучшения в течение нескольких итераций.
В процессе обучения важно мониторить не только функцию потерь на обучающей выборке, но и на валидационной выборке. Это позволяет обнаружить переобучение - ситуацию, когда модель хорошо работает на обучающих данных, но плохо обобщается на новые данные.
Вариации градиентного спуска
Существует несколько вариаций градиентного спуска, каждая со своими преимуществами.
Batch Gradient Descent
Классический градиентный спуск вычисляет градиент на всем наборе данных. Это дает точную оценку градиента, но медленно для больших датасетов. Каждая итерация требует прохода по всем данным.
Stochastic Gradient Descent (SGD)
Стохастический градиентный спуск вычисляет градиент на одном случайном примере. Это быстро, но дает шумную оценку градиента. Шум может помочь выйти из локальных минимумов, но также может замедлить сходимость.
Mini-batch Gradient Descent
Компромисс между batch и SGD. Градиент вычисляется на небольшой подвыборке (обычно 32-256 примеров). Это дает хороший баланс между точностью градиента и скоростью вычислений. Наиболее часто используется на практике.
Adam Optimizer
Адаптивный метод, который автоматически подстраивает скорость обучения для каждого параметра. Использует оценки первого и второго моментов градиента. Часто работает лучше, чем обычный SGD, и требует меньше настройки гиперпараметров.
Momentum
Добавляет "инерцию" к градиентному спуску, накапливая экспоненциально затухающее среднее прошлых градиентов. Это помогает ускорить сходимость в направлениях с постоянным градиентом и сгладить колебания.
RMSprop
Адаптивный метод, который делит скорость обучения на скользящее среднее квадратов градиентов. Это позволяет использовать разные скорости обучения для разных параметров, что особенно полезно для рекуррентных нейронных сетей.
Обратное распространение ошибки
Обратное распространение ошибки (backpropagation) - это эффективный алгоритм вычисления градиентов в нейронных сетях. Он использует цепное правило дифференцирования для вычисления градиента функции потерь по всем параметрам сети за один проход назад через сеть.
Алгоритм работает следующим образом: сначала выполняется прямой проход (forward pass), в котором вычисляются выходы всех слоев сети. Затем выполняется обратный проход (backward pass), в котором градиенты распространяются от выхода к входу, используя цепное правило на каждом слое.
Ключевая идея backpropagation - это повторное использование промежуточных вычислений. Вместо того чтобы вычислять градиент для каждого параметра независимо (что было бы очень медленно), алгоритм вычисляет градиенты последовательно, используя результаты предыдущих вычислений. Это делает обучение глубоких нейронных сетей вычислительно возможным.
Важное уведомление: Этот сайт носит исключительно информационный характер и не предоставляет образовательных услуг.
Пожалуйста, ознакомьтесь с нашими Отказом от ответственности и Политикой конфиденциальности.
