Линейная алгебра
Векторы, матрицы и линейные преобразования - математический фундамент машинного обучения
Введение в линейную алгебру для AI
Линейная алгебра является одним из важнейших разделов математики для понимания искусственного интеллекта и машинного обучения. Она предоставляет язык и инструменты для работы с многомерными данными, которые составляют основу современных алгоритмов машинного обучения. В этом разделе мы рассмотрим ключевые концепции линейной алгебры и их применение в контексте AI.
Почему линейная алгебра важна для машинного обучения?
Машинное обучение работает с данными, которые часто представлены в виде векторов и матриц. Каждый объект данных (например, изображение, текст или числовые характеристики) может быть представлен как вектор в многомерном пространстве. Операции над этими данными - от простого преобразования до сложных вычислений в нейронных сетях - основаны на принципах линейной алгебры.
Понимание векторов, матриц и линейных преобразований позволяет глубже понять, как работают алгоритмы машинного обучения. Например, нейронная сеть по сути представляет собой последовательность матричных умножений и нелинейных преобразований. Без знания линейной алгебры невозможно по-настоящему понять, что происходит "под капотом" этих алгоритмов.
Более того, многие оптимизационные методы, используемые для обучения моделей, также основаны на концепциях линейной алгебры. Градиентный спуск, например, использует векторы градиентов для поиска оптимальных параметров модели. Понимание этих концепций критично для эффективной работы с современными инструментами машинного обучения.
Основные концепции
Давайте рассмотрим фундаментальные понятия линейной алгебры, которые необходимы для понимания машинного обучения.
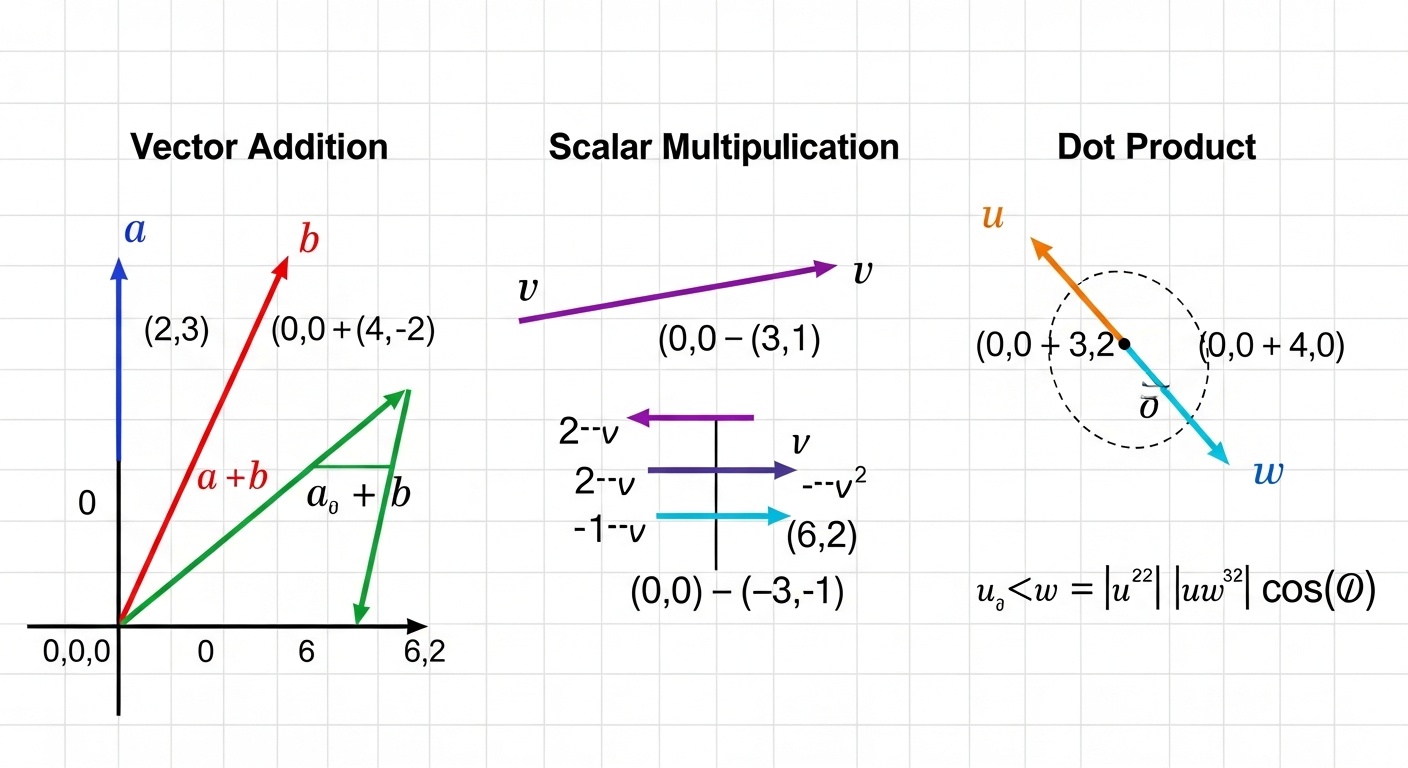
Векторы
Вектор - это упорядоченный набор чисел, который можно представить как точку или направление в многомерном пространстве. В машинном обучении векторы используются для представления признаков объектов. Например, изображение 28x28 пикселей может быть представлено как вектор из 784 чисел.
Векторы поддерживают операции сложения и умножения на скаляр. Скалярное произведение двух векторов - это сумма произведений их соответствующих компонентов, которая имеет важную геометрическую интерпретацию: оно связано с углом между векторами и их длинами.
Матрицы
Матрица - это двумерный массив чисел, организованных в строки и столбцы. Матрицы используются для представления линейных преобразований и наборов данных. В нейронных сетях веса между слоями хранятся в виде матриц.
Матричное умножение - ключевая операция в машинном обучении. Когда мы умножаем матрицу на вектор, мы применяем линейное преобразование к этому вектору. Это лежит в основе работы каждого слоя нейронной сети.
Линейные преобразования
Линейное преобразование - это функция, которая отображает векторы из одного пространства в другое, сохраняя операции сложения и умножения на скаляр. Каждое линейное преобразование может быть представлено матрицей.
В машинном обучении линейные преобразования используются для изменения размерности данных, поворота, масштабирования и других операций. Понимание этих преобразований помогает визуализировать, что происходит с данными на каждом этапе обработки.
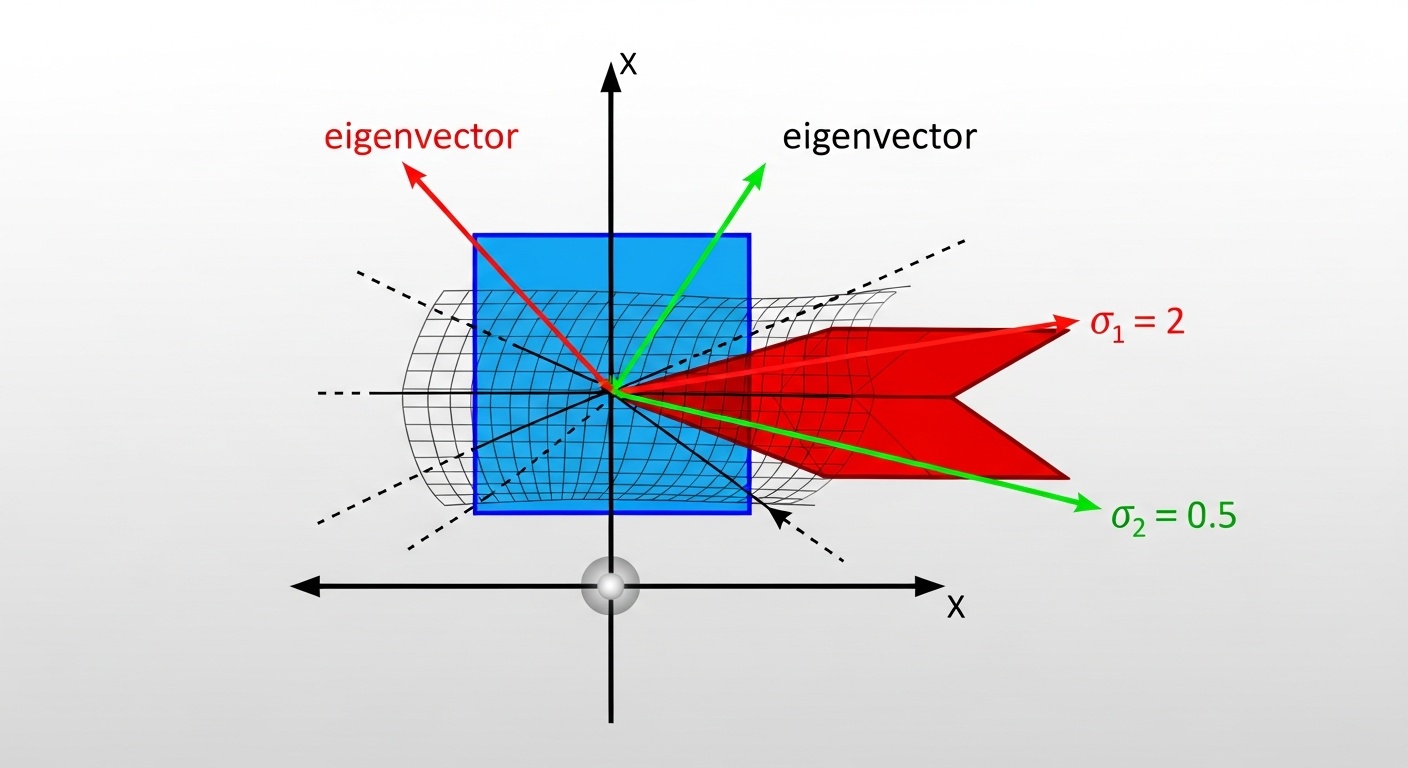
Собственные значения и векторы
Собственный вектор матрицы - это вектор, который при умножении на эту матрицу изменяется только по длине, но не по направлению. Собственное значение показывает, во сколько раз изменяется длина.
Эти концепции критичны для понимания методов снижения размерности, таких как PCA (метод главных компонент), который широко используется для предобработки данных в машинном обучении.
Применение в машинном обучении
Линейная алгебра находит широкое применение во всех областях машинного обучения. Рассмотрим конкретные примеры.
Представление данных
В машинном обучении данные почти всегда представлены в виде векторов и матриц. Каждый объект данных (строка в таблице, изображение, текстовый документ) преобразуется в числовой вектор. Набор данных представляется как матрица, где каждая строка - это один объект, а каждый столбец - это признак.
Например, датасет с информацией о домах может иметь признаки: площадь, количество комнат, год постройки. Каждый дом представлен вектором из трех чисел, а весь датасет - матрицей размером N×3, где N - количество домов.
Нейронные сети
Каждый слой нейронной сети выполняет линейное преобразование входных данных с помощью матричного умножения, за которым следует нелинейная функция активации. Веса нейронной сети хранятся в матрицах, и процесс прямого распространения - это последовательность матричных умножений.
Например, полносвязный слой с 128 входами и 64 выходами использует матрицу весов размером 128×64. Когда входной вектор размером 128 умножается на эту матрицу, получается выходной вектор размером 64. Это базовая операция, которая повторяется миллионы раз при обучении глубоких нейронных сетей.
Снижение размерности
Метод главных компонент (PCA) использует собственные векторы ковариационной матрицы данных для нахождения направлений наибольшей вариации. Это позволяет уменьшить количество признаков, сохраняя при этом большую часть информации.
PCA особенно полезен при работе с высокоразмерными данными, такими как изображения. Вместо работы с тысячами пикселей, мы можем работать с несколькими десятками главных компонент, что значительно ускоряет обучение моделей.
Линейная регрессия
Линейная регрессия - один из базовых алгоритмов машинного обучения - полностью основана на линейной алгебре. Задача состоит в нахождении вектора весов, который наилучшим образом описывает линейную зависимость между признаками и целевой переменной.
Решение задачи линейной регрессии может быть найдено аналитически с использованием операций с матрицами. Формула нормального уравнения включает транспонирование матрицы, матричное умножение и обращение матрицы - все это операции линейной алгебры.
Важные операции и свойства
Рассмотрим ключевые операции линейной алгебры, которые часто используются в машинном обучении.
Матричное умножение
Основная операция в нейронных сетях. Умножение матрицы весов на вектор входных данных дает вектор выходных данных. Важно помнить, что матричное умножение не коммутативно: A×B ≠ B×A.
Транспонирование
Операция, которая меняет местами строки и столбцы матрицы. Транспонирование часто используется в формулах машинного обучения, например, при вычислении градиентов в нейронных сетях.
Обращение матрицы
Обратная матрица A⁻¹ такова, что A×A⁻¹ = I (единичная матрица). Используется в аналитических решениях, таких как нормальное уравнение для линейной регрессии. Не все матрицы имеют обратную.
Норма вектора
Норма измеряет "длину" вектора. L2-норма (евклидова норма) используется для регуляризации моделей и вычисления расстояний между векторами, что важно для алгоритмов кластеризации и классификации.
Скалярное произведение
Скалярное произведение двух векторов дает число, которое связано с углом между ними. Используется для вычисления сходства между векторами, что критично для многих алгоритмов машинного обучения.
Сингулярное разложение (SVD)
Разложение матрицы на произведение трех матриц с особыми свойствами. SVD используется в рекомендательных системах, обработке изображений и снижении размерности данных.
Важное уведомление: Этот сайт носит исключительно информационный характер и не предоставляет образовательных услуг.
Пожалуйста, ознакомьтесь с нашими Отказом от ответственности и Политикой конфиденциальности.
