Математика для искусственного интеллекта
Упрощенное визуальное объяснение ключевых математических концепций, необходимых для понимания машинного обучения и искусственного интеллекта
Ключевые математические концепции
Мы предлагаем упрощенное и визуальное объяснение четырех основных областей математики, которые являются фундаментом для понимания искусственного интеллекта и машинного обучения. Каждая концепция представлена с интерактивными визуализациями и практическими примерами.

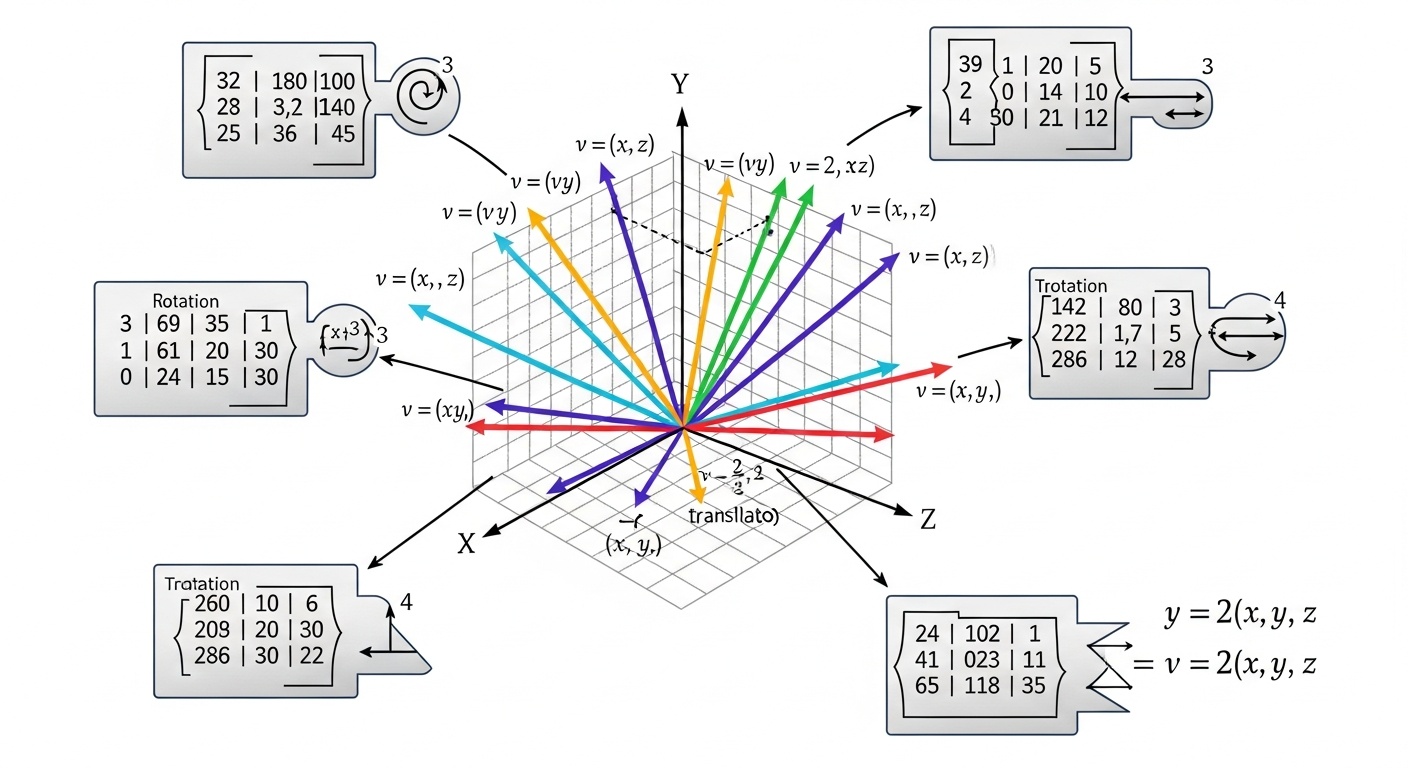
Линейная алгебра
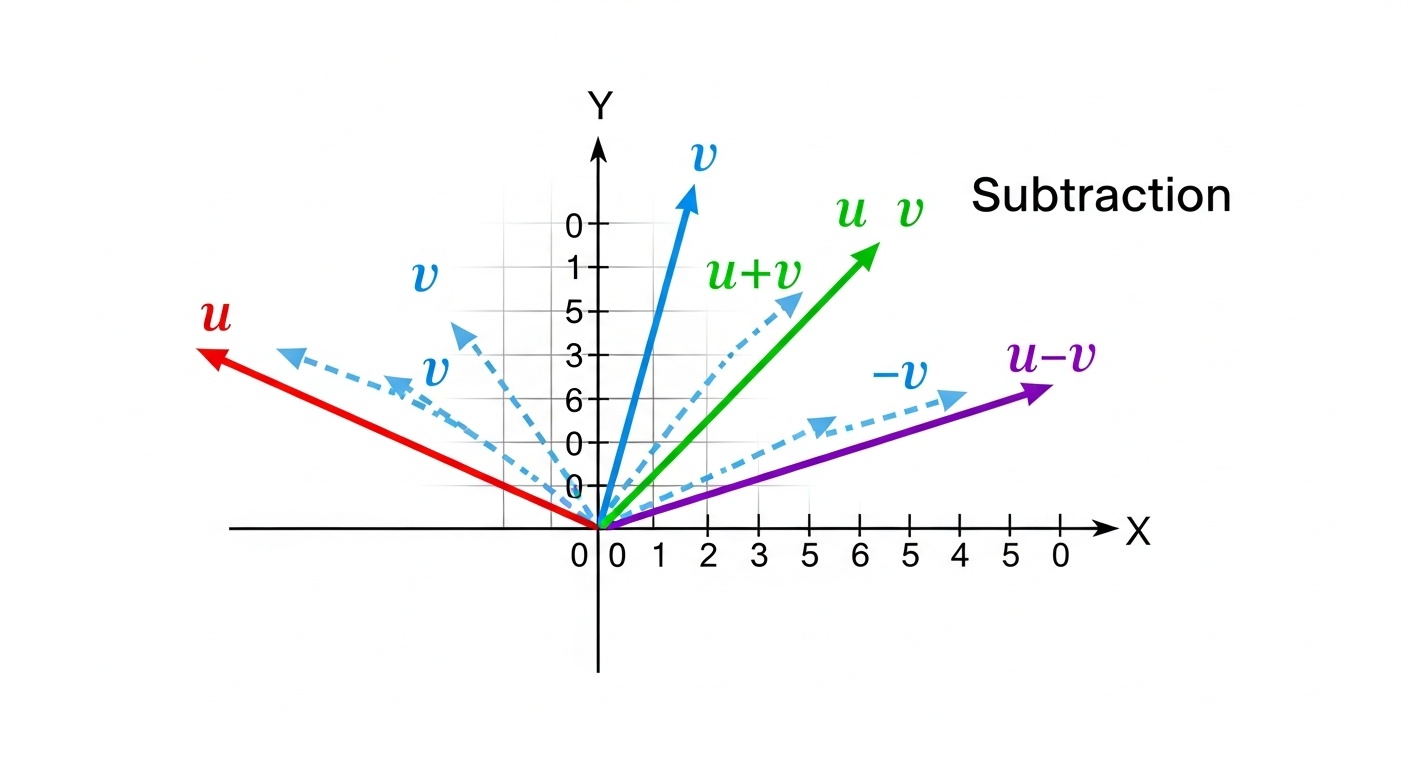
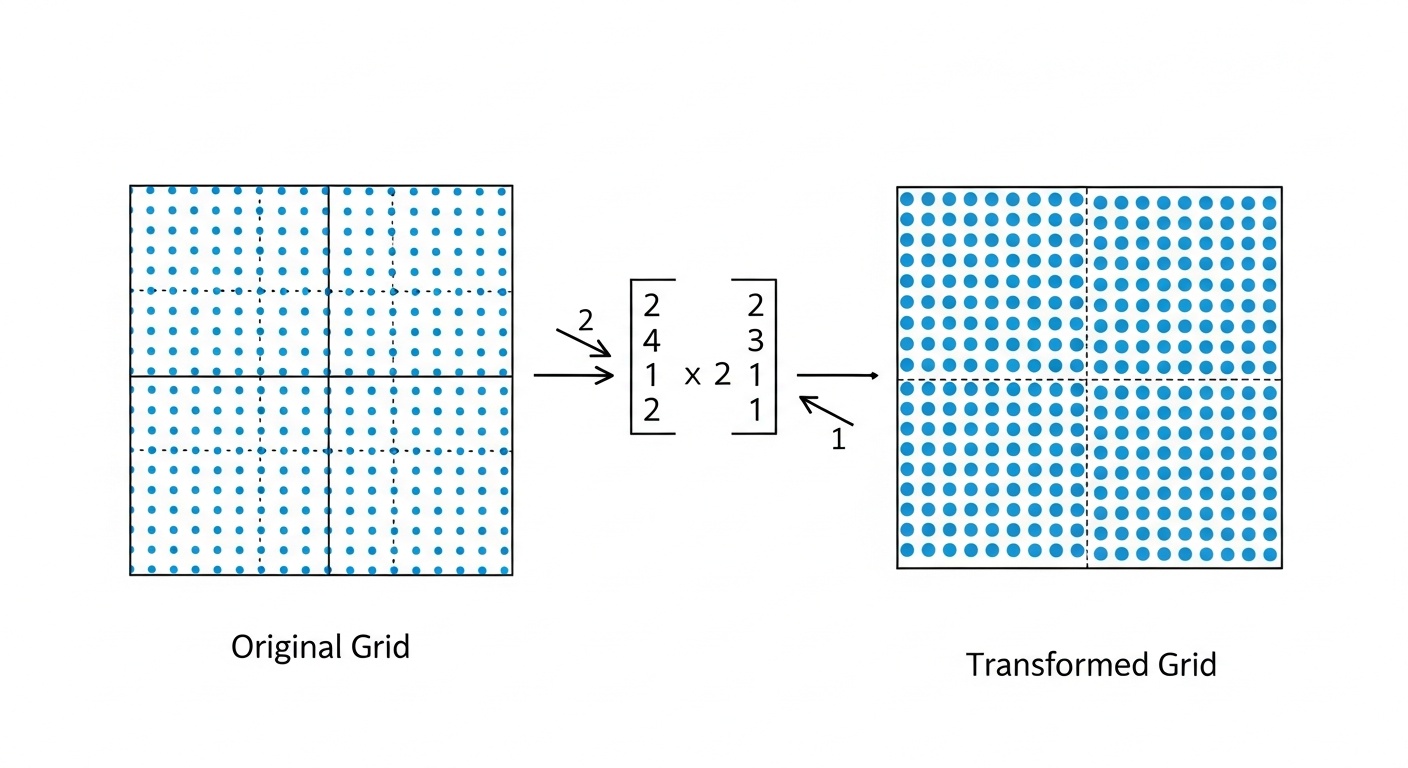
Векторы, матрицы и линейные преобразования - основа для работы с многомерными данными в машинном обучении. Понимание этих концепций критично для глубокого обучения и нейронных сетей.
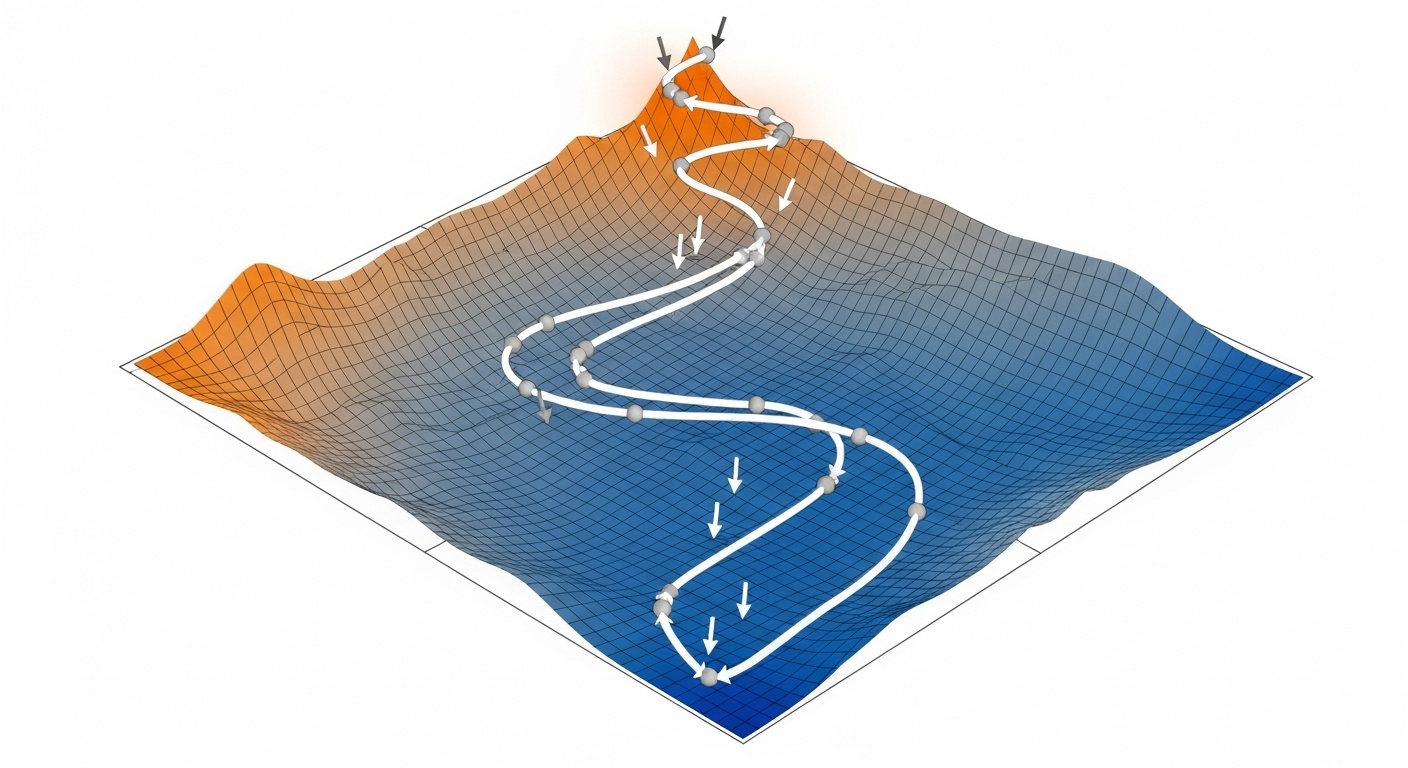
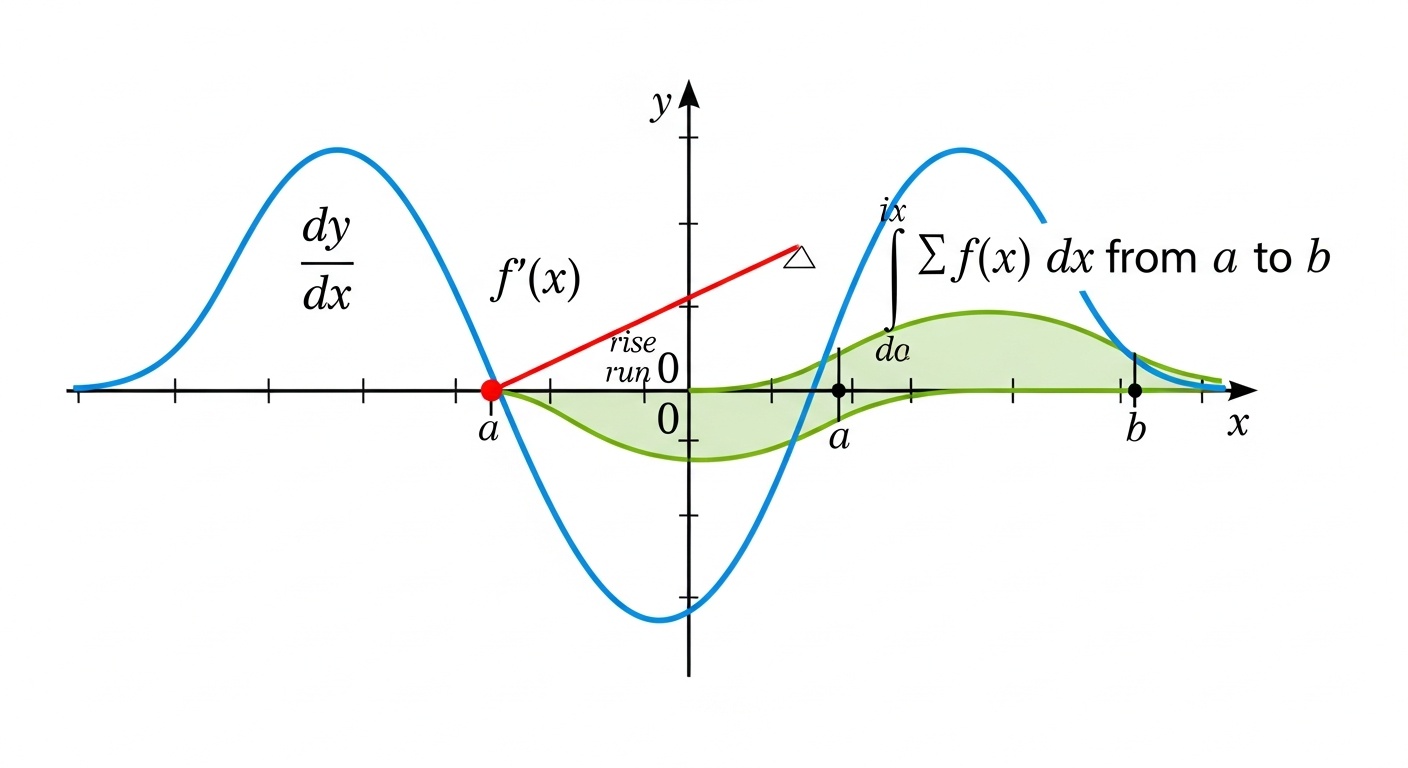
Математический анализ
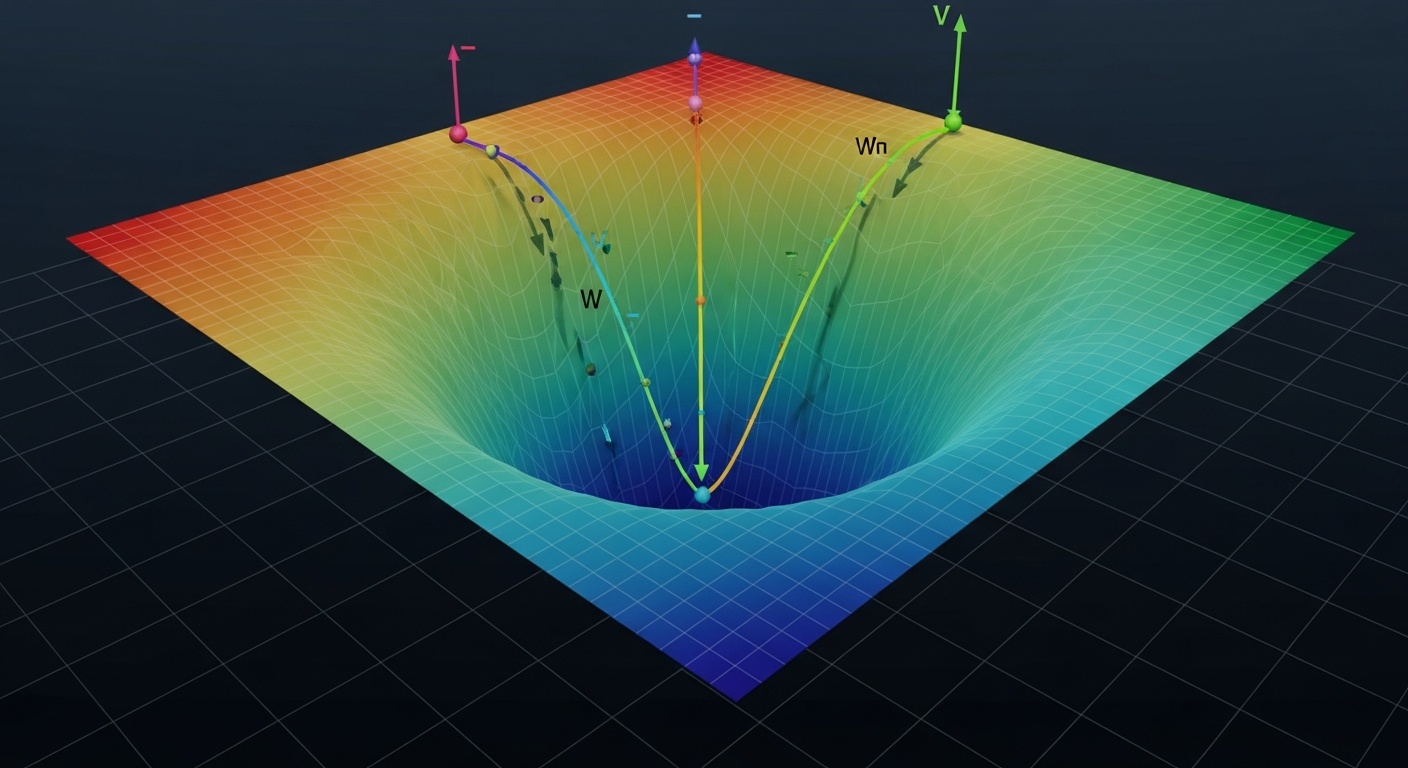
Производные, интегралы и градиенты позволяют оптимизировать модели машинного обучения. Градиентный спуск - ключевой алгоритм обучения нейронных сетей.

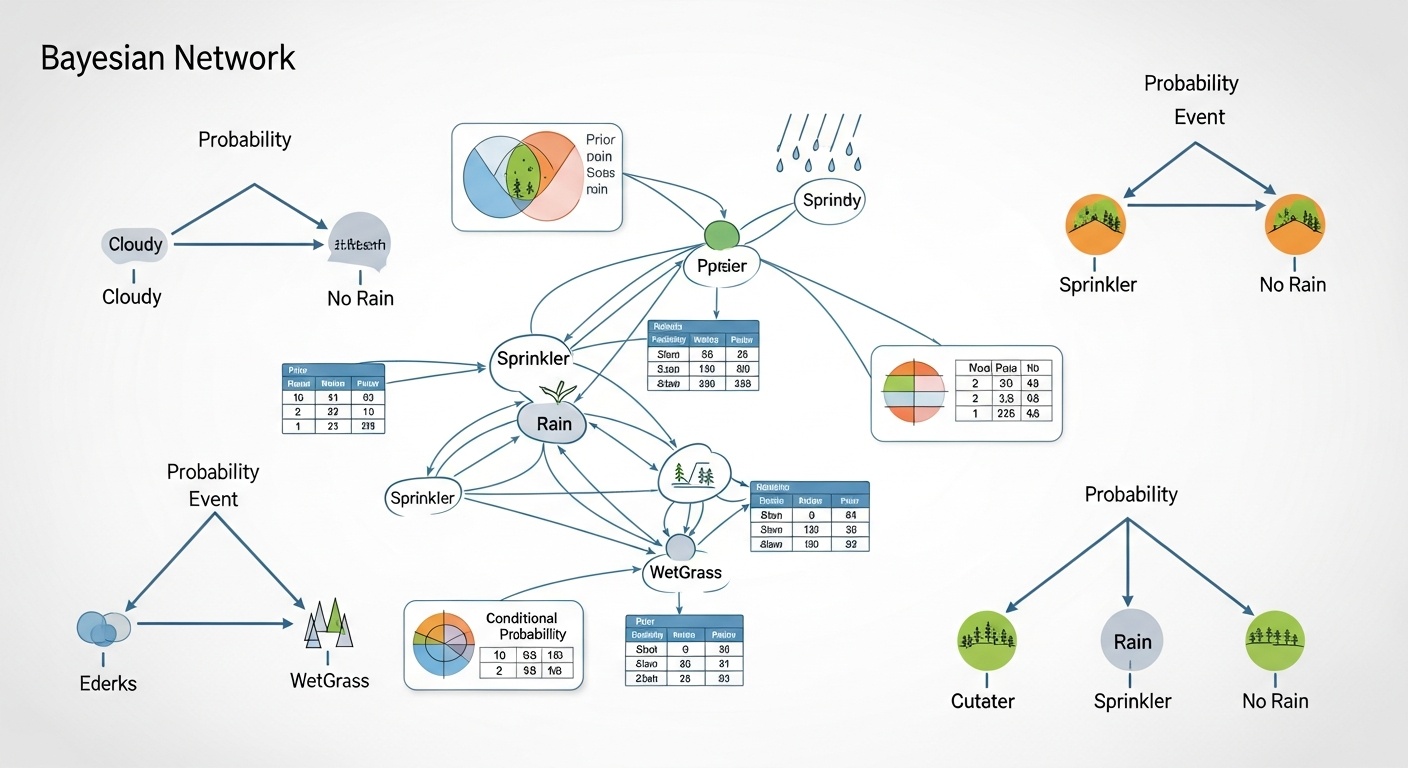
Теория вероятностей
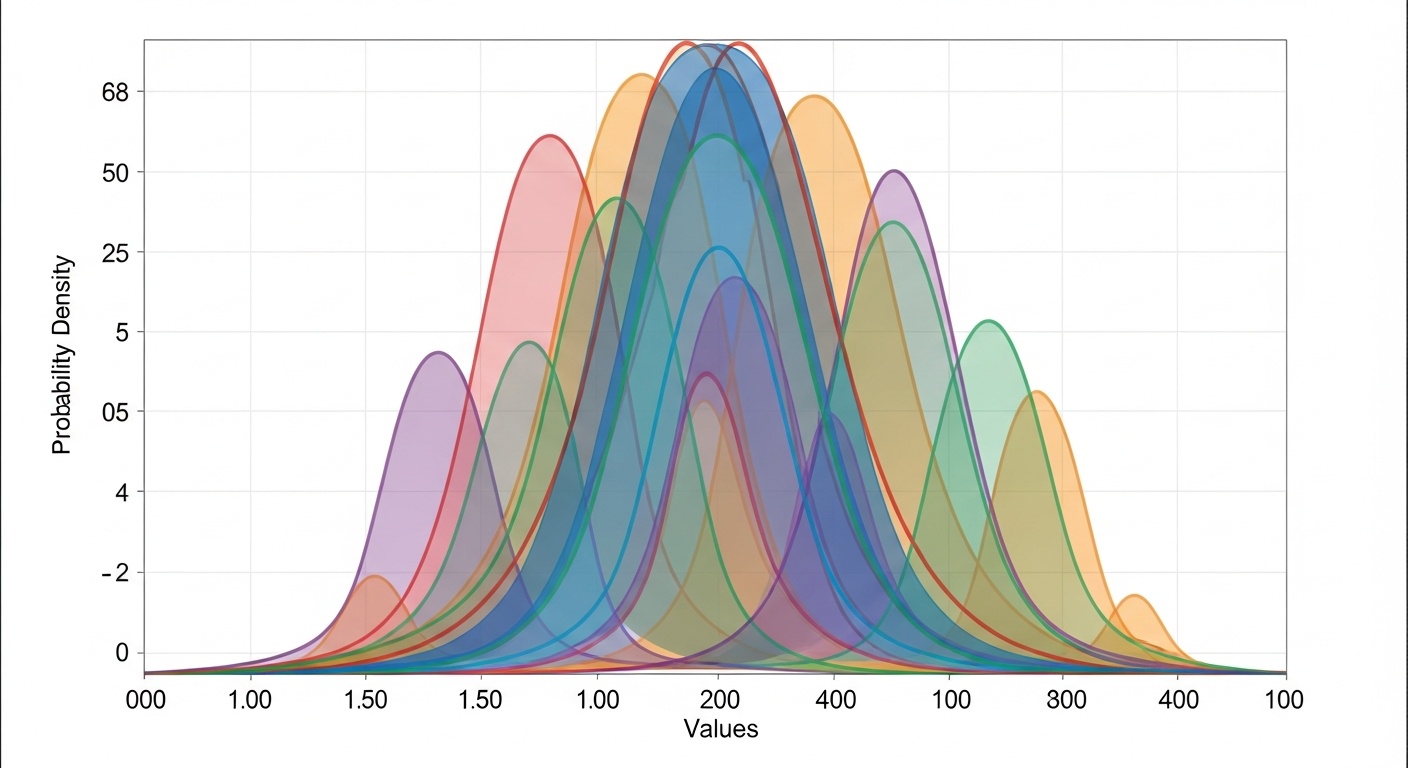
Вероятностные модели и распределения помогают работать с неопределенностью в данных. Байесовские методы широко применяются в машинном обучении.
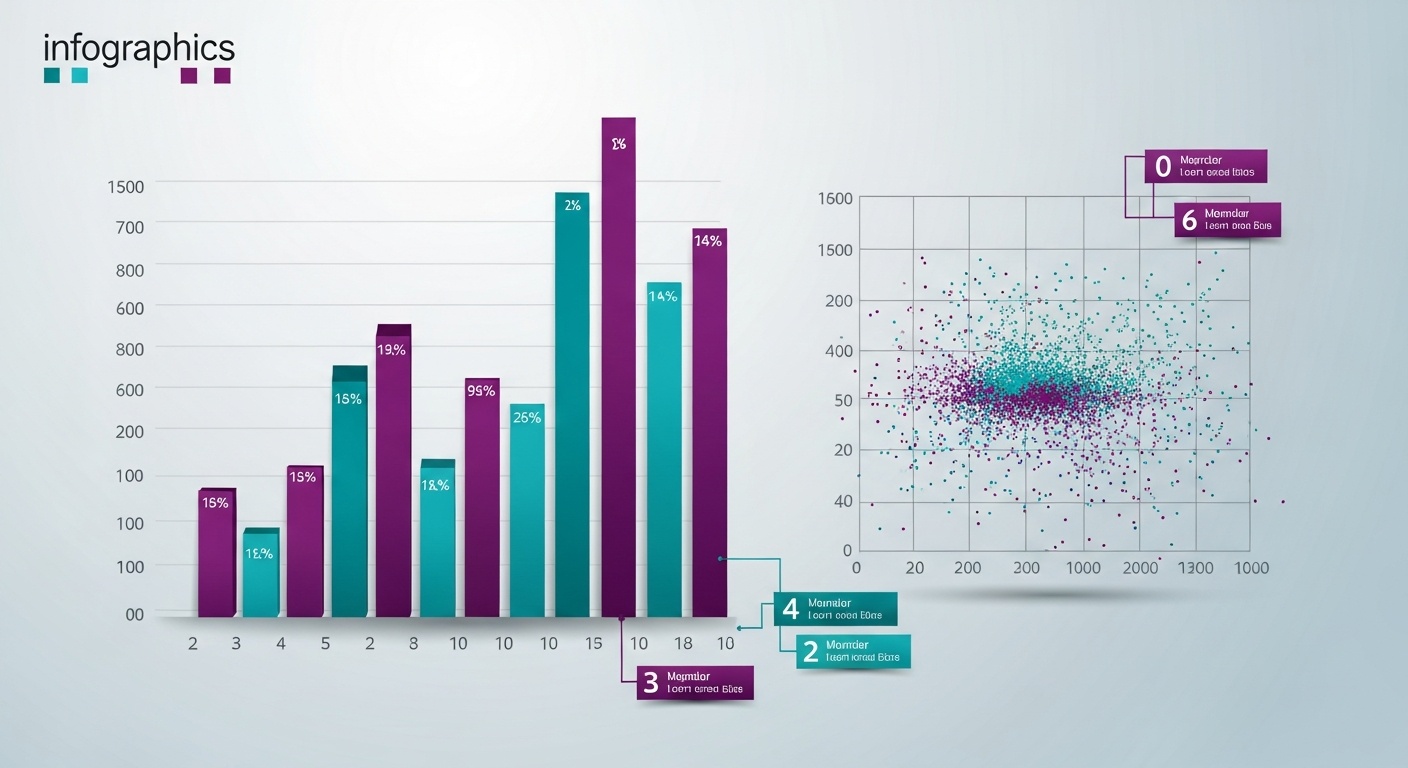
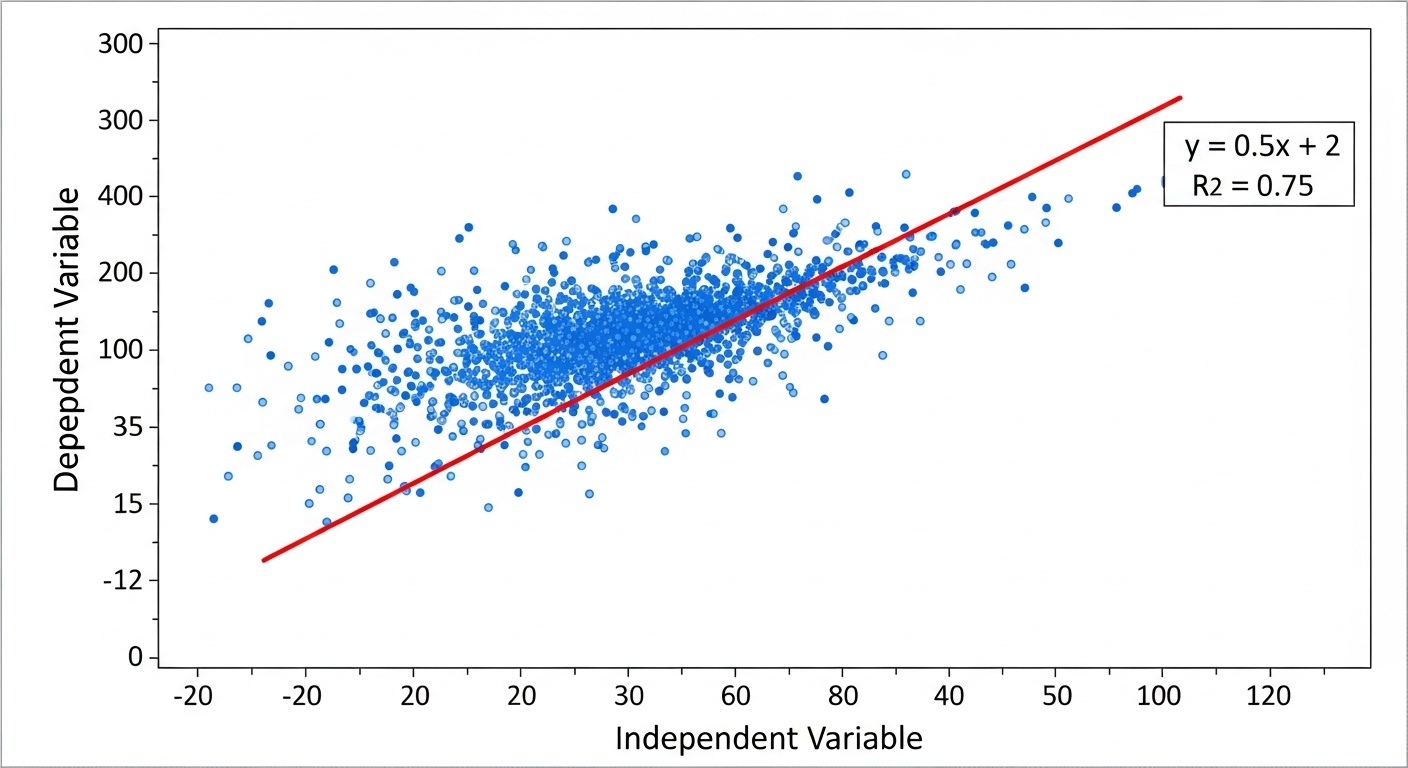
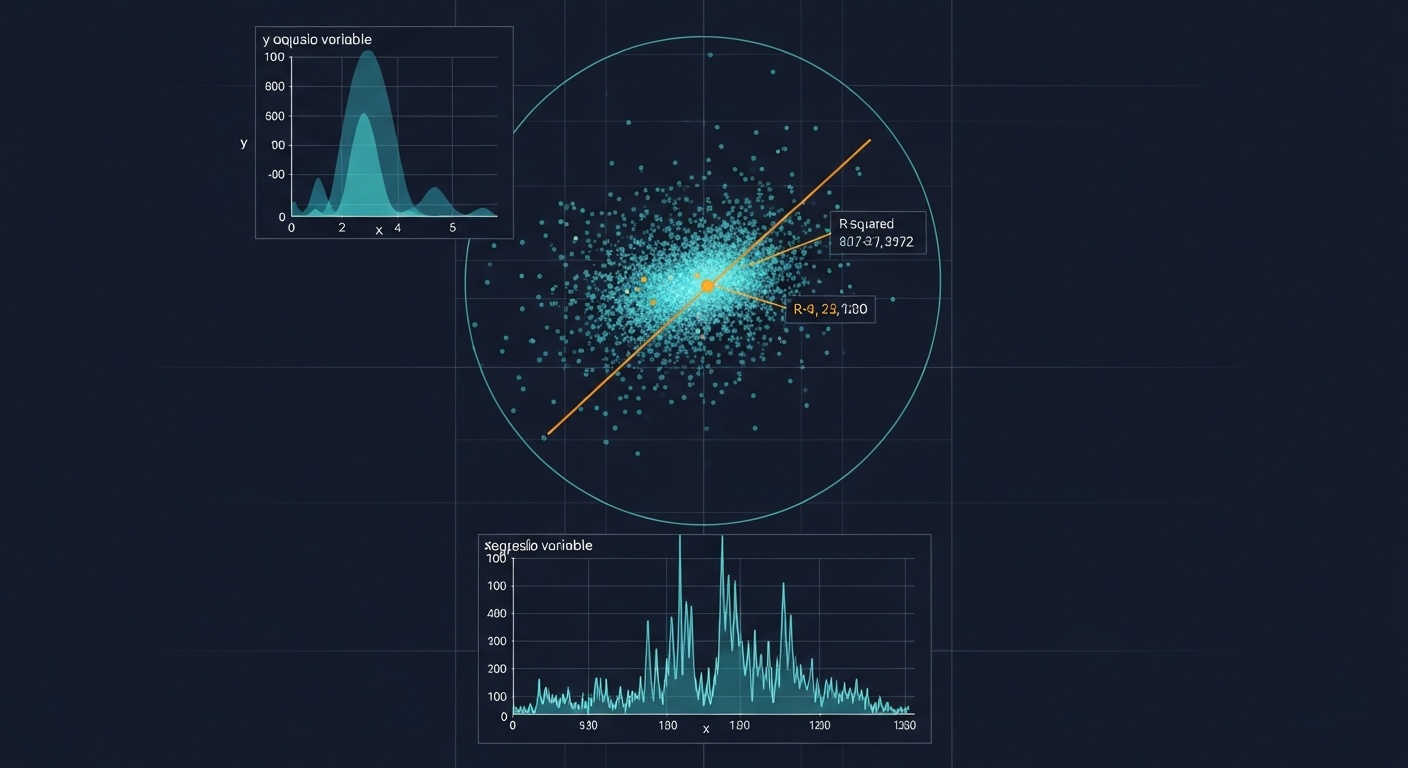
Статистика
Статистический анализ данных, корреляция и регрессия - инструменты для извлечения знаний из данных и построения предсказательных моделей.
Как это работает
Наш подход к обучению математике для AI основан на визуализации и практических примерах. Мы разбиваем сложные концепции на простые, понятные элементы и показываем их применение в реальных задачах машинного обучения.
Шаг 1: Визуальное представление
Мы начинаем с визуального представления математических концепций. Графики, диаграммы и интерактивные визуализации помогают увидеть абстрактные идеи в конкретной форме. Это делает обучение более интуитивным и запоминающимся.
Шаг 2: Упрощенное объяснение
Каждая концепция объясняется простым языком без излишней математической строгости. Мы фокусируемся на интуитивном понимании и практическом применении, а не на формальных доказательствах.
Шаг 3: Связь с AI
Для каждой математической концепции мы показываем конкретные примеры ее применения в машинном обучении и искусственном интеллекте. Это помогает понять, зачем нужна эта математика и как она используется на практике.
Шаг 4: Интерактивные примеры
Интерактивные визуализации позволяют экспериментировать с параметрами и наблюдать, как изменения влияют на результат. Это создает глубокое понимание материала через практический опыт.
Визуальная галерея концепций
Просмотрите нашу коллекцию визуализаций математических концепций, используемых в искусственном интеллекте. Каждое изображение иллюстрирует ключевую идею, которая помогает понять, как работает машинное обучение.
Математика в цифрах
Понимание математики открывает двери в мир искусственного интеллекта. Вот несколько фактов о важности математических концепций в современном машинном обучении.
Часто задаваемые вопросы
Ответы на наиболее распространенные вопросы о математике для искусственного интеллекта и машинного обучения.
Нет, не обязательно знать продвинутую математику на начальном этапе. Наш подход фокусируется на интуитивном понимании ключевых концепций. Мы объясняем математику через визуализации и практические примеры, что делает обучение доступным даже для тех, кто не имеет глубокого математического образования.
Однако базовое понимание линейной алгебры, математического анализа, теории вероятностей и статистики значительно упростит изучение машинного обучения. Именно эти четыре области мы и покрываем на нашем сайте.
Для глубокого обучения особенно важны три области: линейная алгебра, математический анализ и теория вероятностей. Линейная алгебра необходима для понимания операций с тензорами и матричных вычислений, которые лежат в основе нейронных сетей.
Математический анализ, особенно производные и градиенты, критичен для понимания алгоритма обратного распространения ошибки и градиентного спуска. Теория вероятностей помогает работать с неопределенностью и понимать вероятностные модели.
Визуализация превращает абстрактные математические концепции в конкретные, наглядные образы. Когда вы видите, как вектор представлен стрелкой в пространстве, или как градиентный спуск движется по поверхности функции потерь, это создает интуитивное понимание, которое трудно получить только из формул.
Интерактивные визуализации идут еще дальше - они позволяют экспериментировать с параметрами и наблюдать результаты в реальном времени. Это создает глубокое понимание через практический опыт.
Да, наш сайт специально разработан для самостоятельного изучения. Все материалы структурированы от простого к сложному, с множеством примеров и визуализаций. Вы можете изучать темы в своем темпе, возвращаясь к сложным концепциям столько раз, сколько необходимо.
Интерактивные элементы позволяют экспериментировать и проверять свое понимание. Однако помните, что этот сайт носит исключительно информационный характер и не предлагает формальных курсов или сертификации.
Свяжитесь с нами
Есть вопросы о математике для искусственного интеллекта? Хотите узнать больше о наших материалах? Мы всегда рады помочь и ответить на ваши вопросы.
Телефон
Адрес
1750 Howe Ave Suite 300, Sacramento, CA 95825, USA
Информация
Сайт носит информационный характер